Bragg's Law

The structures of crystals and molecules are often being identified using x-ray diffraction studies, which are explained by Bragg’s Law. The law explains the relationship between an x-ray light shooting into and its reflection off from crystal surface.

Introduction

Bragg’s Law was introduced by Sir W.H. Bragg and his son Sir W.L. Bragg. The law states that when the x-ray is incident onto a crystal surface, its angle of incidence, θ$\theta$, will reflect back with a same angle of scattering, θ$\theta$. And, when the path difference, d$d$ is equal to a whole number, n$n$, of wavelength, a constructive interference will occur.

Consider a single crystal with aligned planes of lattice points separated by a distance d. Monochromatic X-rays A, B, and C are incident upon the crystal at an angle θ. They reflect off atoms X, Y, or Z.

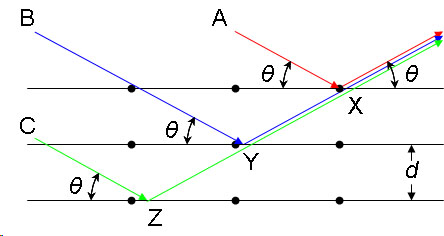
The path difference between the ray reflected at atom X and the ray reflected at atom Y can be seen to be 2YX. From the Law of Sines we can express this distance YX in terms of the lattice distance and the X-ray incident angle:

If the path difference is equal to an integer multiple of the wavelength, then X-rays A and B (and by extension C) will arrive at atom X in the same phase. In other words, given the following conditions:

then the scattered radiation will undergo constructive interference and thus the crystal will appear to have reflected the X-radiation. If, however, this condition is not satisfied, then destructive interference will occur.

Bragg's Law

                       nλ=2dsinθ

where:

• λ is the wavelength of the x-ray,
• d is the spacing of the crystal layers (path difference),
• θ is the incident angle (the angle between incident ray and the scatter plane), and
• n is an integer

The principle of Bragg’s law is applied in the construction of instruments such as Bragg spectrometer, which is often used to study the structure of crystals and molecules.

Selection rules and practical crystallography

Bragg's law, as stated above, can be used to obtain the lattice spacing of a particular cubic system through the following relation:

${\displaystyle d={\frac {a}{\sqrt {h^{2}+k^{2}+l^{2}}}}\,,}$

where ${\displaystyle a}$ is the lattice spacing of the cubic crystal, and ${\displaystyle h}$, ${\displaystyle k}$, and ${\displaystyle l}$ are the Miller indices of the Bragg plane. Combining this relation with Bragg's law:

${\displaystyle \left({\frac {\lambda }{2a}}\right)^{2}=\left({\frac {\lambda }{2d}}\right)^{2}{\frac {1}{h^{2}+k^{2}+l^{2}}}}$

Bravais lattices	Example compounds	Allowed reflections	Forbidden reflections
Simple cubic	Po	Any h, k, l	None
Body-centered cubic	Fe, W, Ta, Cr	h + k + l = even	h + k + l = odd
Face-centered cubic	Cu, Al, Ni, NaCl, LiH, PbS	h, k, l all odd or all even	h, k, l mixed odd and even
Diamond F.C.C.	Si, Ge	all odd, or all even with h+k+l = 4n	h, k, l mixed odd and even, or all even with h+k+l ≠ 4n
Triangular lattice	Ti, Zr, Cd, Be	l even, h + 2k ≠ 3n	h + 2k = 3n for odd l

These selection rules can be used for any crystal with the given crystal structure. KCl has a face-centered cubic Bravais lattice. However, the K⁺ and the Cl⁻ ion have the same number of electrons and are quite close in size, so that the diffraction pattern becomes essentially the same as for a simple cubic structure with half the lattice parameter.